III. Hậu Thiên Bát Quái theo Nguyễn Vũ Tuấn Anh:
1. Đối xứng qua biến đổi f:
Tổng kết và so sánh với Tiên Thiên BQ:
-Theo công thức biểu thị:
+1/8VQ2-T1-8TR2: 1 (f3,8)
+1/2VQ2-T16-1TR16-1TR2: 0
+1/2VQ2-T16: 4 (f5,4; f 5,8; f6,2; f6,8)
+½VQ2-T2-1TR1-1TR2: 0
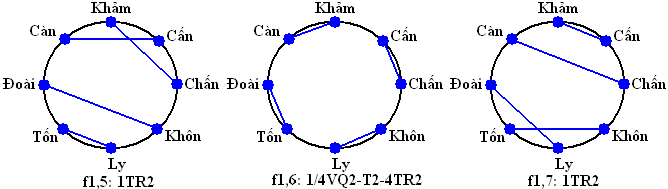
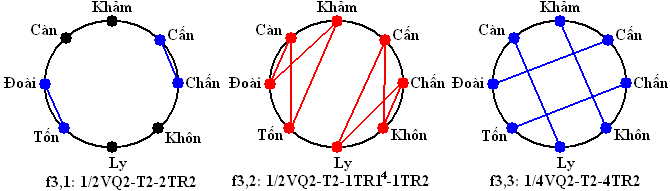
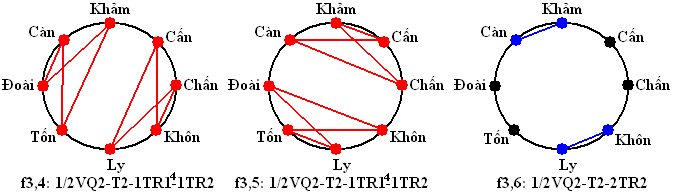
+1/2VQ2-T2-1TR14-1TR2: 4 (f3,2, f3,4, f3,5, f3,7)
+1/4VQ2-T2-4TR2: 2 (f1,6, f3,3)
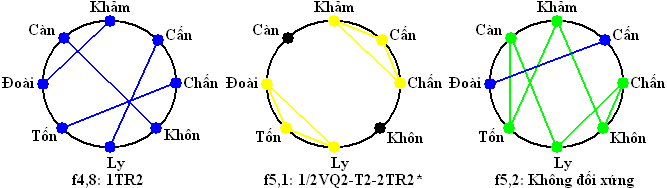
+1/2VQ2-T2-2TR2: 6 (f1,3, f1,8, f3,1, f3,6, f5,1, f6,1)
+1/2VQ2-T2: 2 (f5,5, f6,7)
+1TR14: 4 (f2,6, f2,7, f4,5, f4,6)
+1TR2: 6 (f1,2, f1,4, f1,5, f1,7, f2,8, f4,8)
+Không đối xứng: 18 (f2,1, f2,2, f2,3, f2,4, f2,5, f4,1, f4,2, f4,3, f4,4, f4,7, f5,2, f5,3, f5,6, f5,7, f6,3, f6,4, f6,5, f6,6).
-Tổng các chi tiết (elements) đối xứng:
+T1: 1.
+T16: 4.
+TR1: 0.
+TR14: 8
+TR16: 0
+T2: 14
+TR2:38
-Có phần lớn các đồ hình biến đổi qua f mang tính đối xứng cao. Thế nhưng vẫn còn rất nhiều đồ hình (đến 18) không đối xứng. Chính vì thế, tổng các chi tiết đối xứng chỉ được 65 xấp xỉ một nửa của Tiên thiên Bát Quái. Nếu so với Bát Quái Văn Vương thì bát quái này trội hơn hẳn. Ngoài 35 chi tiết đối xứng chênh lệch, bát quái này còn hơn hẳn về chất, như có T1, có T1(6), có nhiều T2….
-Về triết học, cũng có thể giải thích khá vẹn toàn: nếu cho Thiên và Địa và hai chiều đối nghịch nhau thì, bát quái hậu thiên mang đối xứng T1 qua biến đổi: vừa quay các quái một góc 180 độ vừa phủ định cả các vạch sẽ cho ra quái đối diện.
-Tuy nhiên, chúng tôi cho đây cũng không phải là Hậu Thiên Bát Quái nguyên thuỷ bởi nhiều lý do mà chúng tôi sẽ trình bày trong những chương sau. Sự khác xa khá bất thường của nó đối với Tiên Thiên cũng đủ để chúng ta nghi ngờ tính chuẩn xác của bát quái này.
![[THẾ GIỚI VÔ HÌNH] - Mã nguồn vBulletin](images/misc/vbulletin4_logo.png)
















 Trả lời ngay kèm theo trích dẫn này
Trả lời ngay kèm theo trích dẫn này
Bookmarks